Inhalt
In der Mathematik wird das Studium von Dreiecken als Trigonometrie bezeichnet. Alle unbekannten Werte von Winkeln und Seiten können unter Verwendung der üblichen trigonometrischen Identitäten von Sinus, Cosinus und Tangens entdeckt werden. Diese Identitäten sind einfache Berechnungen, mit denen die Seitenverhältnisse in Winkelgrade umgerechnet werden. Unbekannte Winkel werden als bezeichnet Winkel Theta und kann auf verschiedene Arten basierend auf bekannten Seiten und Winkeln berechnet werden.
Rechte Dreiecke
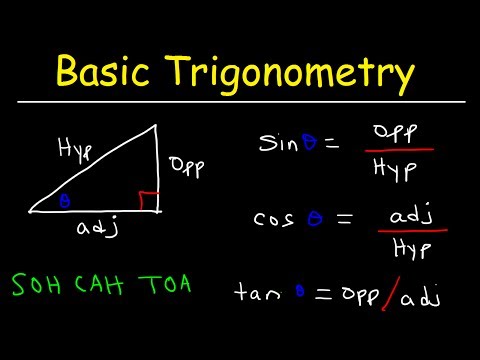
Wenn ein Dreieck einen Winkel von 90 Grad enthält, wird es als a bezeichnet rechtwinkliges Dreieckund der Winkel Theta können unter Verwendung des Akronyms bestimmt werden SOHCAHTOA.
In zerlegtem Zustand bedeutet dies, dass Sinus (S) gleich der Länge des gegenüberliegenden Winkels Theta (O) geteilt durch die Länge der Hypotenuse (H) ist, so dass Sinus (X) = Opp / Hyp. In ähnlicher Weise ist Cosinus (C) gleich der Länge der benachbarten Seite (A) geteilt durch die Hypotenuse. (H) Cos (X) = Adj / Hyp. Tangens (T) ist gleich dem Gegenteil (O) geteilt durch das benachbarte (A). Tan (X) = Opp / Adj.
Um diese Verhältnisse mit einem Grafikrechner zu lösen, verwenden Sie die inversen Triggerfunktionen, die als bekannt sind Arcsin, Arccos und arctan - und auf dem Rechner als SIN ^ -1, COS ^ -1 und TAN ^ -1 dargestellt.
Wenn die Länge der Gegenseite sowie die Hypotenuse bekannt sind, die dem SOH im Akronym entspricht, verwenden Sie die Arcussin-Funktion des Rechners und geben Sie die beiden Längen in Bruchform ein.
Beispiel: Wenn der gegenüberliegende Winkel Theta eine Länge von 4 und die Hypotenuse eine Länge von 5 hat, geben Sie das Verhältnis folgendermaßen in den Rechner ein:
SIN ^ -1 (4/5)
Dies sollte einen Wert von ungefähr 53,13 Grad ergeben. Ist dies nicht der Fall, vergewissern Sie sich, dass sich der Rechner im DEGREE-Modus befindet, und versuchen Sie es erneut.
Gesetz der Sines
Wenn in einem Dreieck keine 90-Grad-Winkel vorhanden sind, hat SOHCAHTOA beim Auflösen nach Winkeln keine Bedeutung. Wenn jedoch ein Winkel und die Länge seiner Gegenseite bekannt sind, kann die Gesetz der Sines kann in Zusammenarbeit mit einer anderen bekannten Seitenlänge verwendet werden, um fehlende Winkel zu finden. Das Gesetz besagt, dass sin A / a = sin B / b = sin C / c.
Zusammengefasst bedeutet dies, dass der Sinus eines Winkels geteilt durch die Länge seiner gegenüberliegenden Seite direkt proportional zum Sinus eines anderen Winkels geteilt durch die Länge seiner gegenüberliegenden Seite ist. Um dies zu lösen, isolieren Sie den Sinus des unbekannten Winkels, indem Sie beide Seiten der Gleichung mit der Länge des Winkels auf der gegenüberliegenden Seite multiplizieren.
Zum Beispiel: sin A / a = sin B / b wird (b * sin A) / a = sin B
In einem Taschenrechner, der Seite a = 5, Seite b = 7 und Winkel A = 45 Grad gegeben ist, wird dies als SIN ^ -1 ((7 · SIN (45)) / 5) angesehen. Dies gibt dem Winkel B einen Wert von ungefähr 81,87 Grad.
Gesetz des Kosinus
Das Gesetz des Kosinus Funktioniert auf allen Dreiecken, wird jedoch hauptsächlich in Fällen verwendet, in denen die Längen aller Seiten bekannt sind, aber keiner der Winkel bekannt ist. Die Formel ist ähnlich der Satz des Pythagoras (a ^ 2 + b ^ 2 = c ^ 2) und gibt c ^ 2 = a ^ 2 + b ^ 2 - 2ab * cos (C) an. Zum Auffinden von Theta ist es jedoch einfacher, cos (C) = (a ^ 2 + b ^ 2 - c ^ 2) / 2ab zu lesen.
Wenn ein Dreieck beispielsweise drei Seiten hat, die 5, 7 und 10 messen, geben Sie diese Werte als cos ^ -1 ((5 ^ 2 + 7 ^ 2 - 10 ^ 2) / (2_5_7)) in einen Grafikrechner ein. Diese Berechnung gibt einen Wert von ungefähr 111,80 Grad aus.
Übe für die Meisterschaft
Es ist wichtig, sich daran zu erinnern, dass alle Dreiecke aus drei Winkeln mit einer Gesamtsumme von 180 Grad bestehen. Üben Sie die verschiedenen Techniken an verschiedenen Dreiecken, bis Sie mit dem Vorgang vertraut sind. Manchmal ist das Entdecken von Theta dasselbe wie das Entdecken einer neuen Methode, um das Problem zu umgehen.