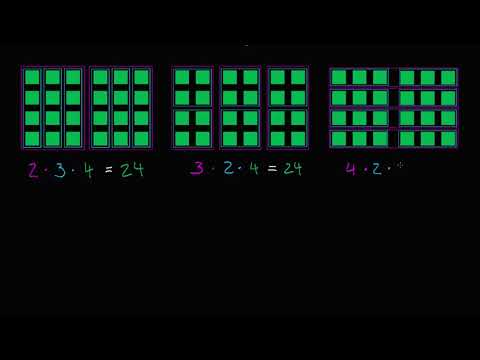
Inhalt
Einfach ausgedrückt bedeutet die kommutative Eigenschaft der Multiplikation, dass Sie unabhängig von der Reihenfolge der zu multiplizierenden Zahlen die gleiche Antwort erhalten. Addition teilt auch die kommutative Eigenschaft mit Multiplikation, während Division und Subtraktion dies nicht tun. Wenn Sie beispielsweise 3 mit 5 oder 5 mit 3 multiplizieren, erhalten Sie dieselbe Antwort von 15.
Grundlagen zu kommutativen Eigenschaften
Das Wurzelwort für "kommutativ" ist "pendeln". Sie können sich an die Bedeutung von kommutativ erinnern, indem Sie an die Definition von "pendeln" denken, was bedeutet, sich zu bewegen, Orte zu wechseln, zu reisen oder zu tauschen. Das Produkt ist unabhängig von der Reihenfolge der Faktoren gleich. Wenn Sie beim Addieren 5 und 3 oder 3 und 5 addieren, erhalten Sie die gleiche Summe von 8. Gleiches gilt für die Multiplikation: Die Reihenfolge der Faktoren spielt keine Rolle.
Beispielprobleme
Die Beispiele von 3 × 5 = 15 und 5 × 3 = 15 sind numerische Beispiele für die kommutative Eigenschaft, die mit der Multiplikation verbunden ist. Dies kann auch durch ein Array veranschaulicht werden. Zeichnen Sie auf ein Blatt Papier 15 Kreise, aber ordnen Sie sie in Spalten und Reihen an. Unabhängig davon, ob Sie drei Reihen mit fünf Kreisen oder fünf Reihen mit drei Kreisen erstellt haben, entsprechen beide Anordnungen 15 Kreisen. Die gleiche Logik gilt für algebraische Begriffe wie ab = ba oder (4x) (2y) = (2y) (4x).
Wortprobleme
Obwohl sowohl Addition als auch Multiplikation die kommutative Eigenschaft haben, sind die Interpretationen etwas unterschiedlich, wenn Sie solche Operationen nach dem Lesen von Wortproblemen ausführen müssen. Wenn Sie ein Wortproblem lesen, bei dem 112 Häuser mit 134 Häusern hinzugefügt werden, ändert sich die Bedeutung unabhängig von der Reihenfolge, in der Sie die Zahlen hinzufügen. Angenommen, Sie werden aufgefordert, die Gesamtzahl der Blumen zu bestimmen: Wenn das Wort problem fünf Gruppen von vier Blumen angibt, sollten Sie die Gleichung als 5 x 4 interpretieren. Wenn das Problem aus vier Fünfergruppen besteht, sollten Sie 4 x 5 multiplizieren. Obwohl die Antworten gleich sind, lohnt es sich, sich die Zeit zu nehmen, ein Wortproblem langsam zu lesen, um die genaue Frage zu verstehen. Sie können die Gruppierungen sogar zeichnen, bevor Sie Ihre endgültige Antwort erstellen.
Verwandte Eigenschaften
Einige mathematische Eigenschaften gehen mit der kommutativen Eigenschaft einher. Die assoziative Eigenschaft bezieht sich auch sowohl auf die Addition als auch auf die Multiplikation. Wenn Sie bei der Multiplikation drei oder mehr Faktoren haben, spielt die Reihenfolge und Gruppierung der Faktoren keine Rolle - das Produkt ist immer dasselbe. Zum Beispiel ist (2 x 3) x 4 dasselbe wie (3 x 4) x 2 und entspricht jeweils 24. Die Verteilungseigenschaft bezieht sich nur auf die Multiplikation. Gemäß dieser Eigenschaft ist die Summe von zwei Zahlen multipliziert mit einer dritten Zahl die gleiche wie die Multiplikation jeder der Zahlen, die mit diesem Faktor addiert werden. In algebraischen Begriffen kann dies durch x (y + z) = xy + xz dargestellt werden.