
Inhalt
Damit zwei Formen kongruent sind, muss jede die gleiche Anzahl von Seiten haben und ihre Winkel müssen auch gleich sein. Die einfachste Methode, um festzustellen, ob zwei Formen kongruent sind, besteht darin, eine der Formen zu drehen, bis sie an der anderen ausgerichtet ist, oder die Formen einfach übereinander zu stapeln, um festzustellen, ob Enden hervorstehen. Wenn Sie die Formen nicht physisch verschieben können, können Sie mithilfe von Formeln feststellen, ob die Formen kongruent sind.
Kongruente Kreise
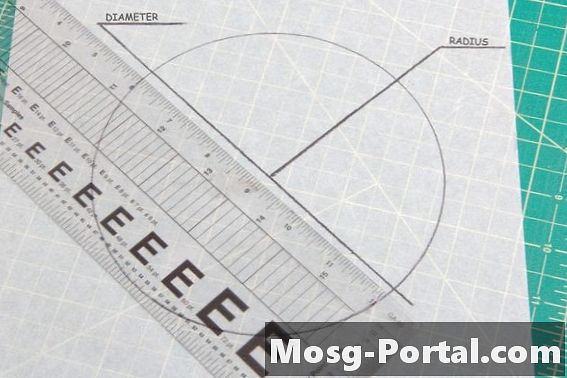
••• Ray Robert Green / Medien nachfragenAlle Kreise haben den gleichen Winkel von 360 Grad. Der einzige Faktor bei der Bestimmung der Kongruenz zweier Kreise ist der Vergleich ihrer Größe. Der Durchmesser ist eine gerade Linie durch die Mitte des Kreises von Kante zu Kante, während der Radius eines Kreises die Länge von seiner Mitte zu seiner Außenkante ist. Wenn Sie einen dieser Werte in beiden Kreisen messen, wird geprüft, ob sie kongruent sind.
Parallelogramme
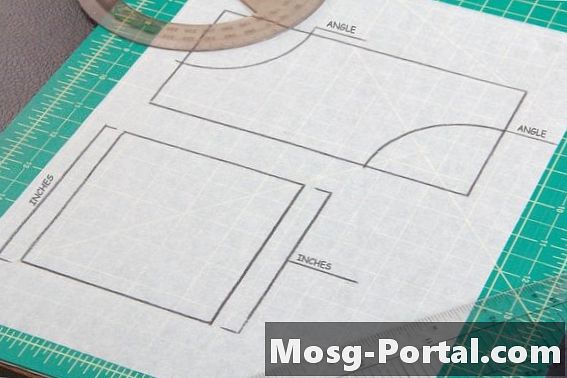
Ein Parallelogramm besteht aus zwei Paaren paralleler Seiten, z. B. Quadraten und Rechtecken. Die gegenüberliegenden Seiten oder Winkel eines Parallelogramms haben dasselbe Maß, daher ist es erforderlich, zwei Winkel- oder Seitenmessungen an einem Parallelogramm vorzunehmen, eine von jedem Seitenpaar, um die Kongruenz mit einer anderen Form zu vergleichen.
Dreiecke
••• Ray Robert Green / Medien nachfragenUm die Kongruenz von Dreiecken zu finden, müssen Sie die Größe jedes Winkels oder jeder Seite bestimmen, da alle drei unterschiedlich sein können. Es gibt drei Postulate, mit denen kongruente Dreiecke identifiziert werden können. Das SSS-Postulat ist, wenn Sie alle drei Seiten eines jeden Dreiecks messen. Das ASA-Postulat besagt, wenn zwei Winkel und ihre Verbindungsseite mit denen des anderen Dreiecks übereinstimmen, sind sie kongruent. Das SAS-Postulat macht das Gegenteil: Es misst zwei Seiten und ihren Verbindungswinkel, um sie mit dem anderen Dreieck zu vergleichen.
Theoreme für kongruente Dreiecke

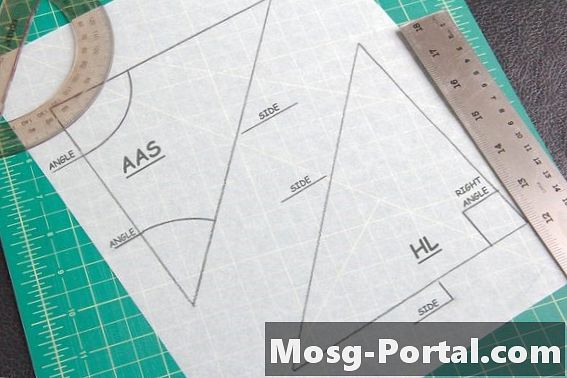
Zwei Sätze sind nützlich, um kongruente Dreiecke zu finden. Das AAS-Theorem besagt, dass wenn zwei Winkel und eine Seite, die die beiden nicht verbindet, gleich dem eines anderen Dreiecks sind, sie kongruent sind. Der Hypotenuse-Leg-Satz gilt nur für Dreiecke mit einem 90-Grad- oder "rechten" Winkel. In diesem Fall messen Sie die Hypotenuse - die dem 90-Grad-Winkel gegenüberliegende Seite - und eine der anderen Seiten des Dreiecks, um sie mit der anderen Form zu vergleichen.