Inhalt
In der Geometrie ist ein Achteck ein Polygon mit acht Seiten. Ein regelmäßiges Achteck hat acht gleiche Seiten und gleiche Winkel. Das regelmäßige Achteck wird üblicherweise an Stoppschildern erkannt. Ein Oktaeder ist ein achteckiges Polyeder. Ein regelmäßiges Oktaeder hat acht Dreiecke mit gleich langen Kanten. Es sind effektiv zwei quadratische Pyramiden, die sich an ihren Basen treffen.
Achteck-Bereichsformel
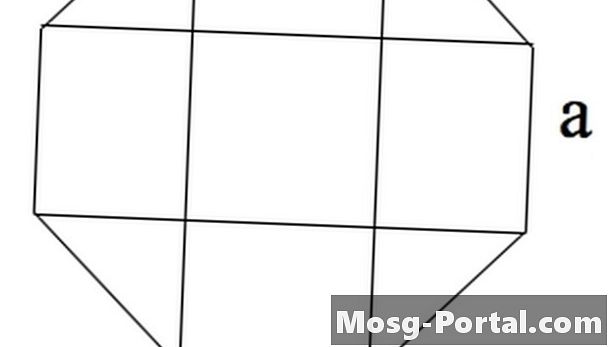
Die Formel für die Fläche eines regelmäßigen Achtecks mit Seiten der Länge "a" lautet 2 (1 + sqrt (2)) a ^ 2, wobei "sqrt" die Quadratwurzel angibt.
Ableitung
Ein Achteck kann als 4 Rechtecke, ein Quadrat in der Mitte und vier gleichschenklige Dreiecke in den Ecken betrachtet werden.
Das Quadrat hat die Fläche a ^ 2.
Die Dreiecke haben die Seiten a, a / sqrt (2) und a / sqrt (2) nach dem Satz von Pythagoras. Daher hat jeder eine Fläche von a ^ 2/4.
Die Rechtecke haben die Fläche a * a / sqrt (2).
Die Summe dieser 9 Bereiche ist 2a ^ 2 (1 + sqrt (2)).
Octahedron Volume Formula
Die Formel für das Volumen eines regelmäßigen Oktaeders der Seiten "a" lautet ^ 3 * sqrt (2) / 3.
Ableitung
Die Fläche einer vierseitigen Pyramide ist Grundfläche * Höhe / 3. Die Fläche eines regelmäßigen Achtecks ist daher 2 * Grundfläche * Höhe / 3.
Basis = a ^ 2 trivial.
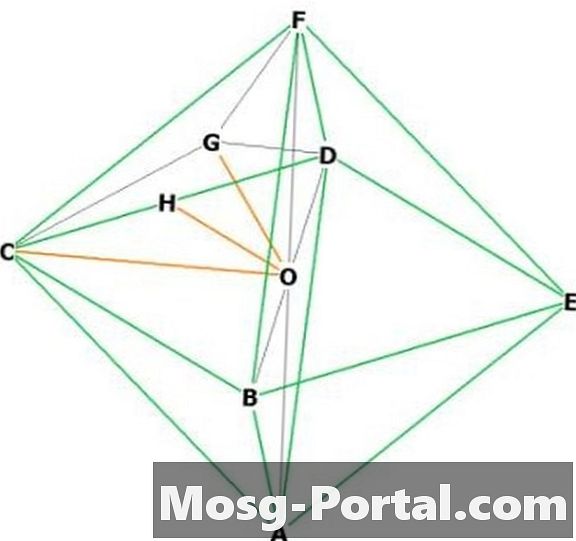
Wählen Sie zwei benachbarte Eckpunkte aus, sagen Sie "F" und "C". "O" ist in der Mitte. FOC ist ein gleichschenkliges rechtwinkliges Dreieck mit der Basis "a", also haben OC und OF die Länge a / sqrt (2) nach dem Satz von Pythagoras. Also Höhe = a / sqrt (2).
Das Volumen eines regulären Oktaeders ist also 2 * (a ^ 2) * a / sqrt (2) / 3 = a ^ 3 * sqrt (2) / 3.
Oberfläche
Die regelmäßige Oktaederfläche ist die Fläche eines gleichseitigen Dreiecks der Seite "a" mal 8 Flächen.
Um den Satz von Pythagoras zu verwenden, ziehen Sie eine Linie vom Scheitelpunkt zur Basis. Dies erzeugt zwei rechtwinklige Dreiecke mit der Hypotenuse der Länge "a" und einer Seitenlänge "a / 2". Daher muss die dritte Seite sqrt = sqrt (3) a / 2 sein. Die Fläche eines gleichseitigen Dreiecks ist also Höhe * Basis / 2 = Sqrt (3) a / 2 * a / 2 = Sqrt (3) a ^ 2/4.
Mit 8 Seiten beträgt die Oberfläche eines regulären Oktaeders 2 * sqrt (3) * a ^ 2.