
Ein logarithmisches Diagramm, das formal als semi-logarithmisches Diagramm bezeichnet wird, verwendet eine lineare Skala auf einer Achse und eine logarithmische Skala auf der anderen Achse. Es ist in der Wissenschaft nützlich, um Datenpunkte von zwei Variablen zu zeichnen, wobei eine der Variablen einen viel größeren Wertebereich als die andere Variable aufweist. Durch das Aufzeichnen der Daten auf diese Weise können wir häufig Beziehungen in den Daten beobachten, die nicht so offensichtlich wären, wenn beide Variablen linear aufgezeichnet würden.
Definieren Sie einen Logarithmus. Für die Gleichung x = b ^ y würden wir sagen, dass y der Logarithmus von x zur Basis b ist. Wenn also x = b ^ y, dann ist y = logb (x).
Stellen Sie lineare und logarithmische Skalen auf. Die Markierungen auf einer linearen Skala zeigen einzelne Einheiten und sind mit 1, 2, 3, 4 usw. gekennzeichnet. Die Markierungen auf einer logarithmischen Skala zeigen Potenzen der Logarithmenbasis. Beispielsweise würde eine logarithmische Skala mit einer Basis von 10 mit 10, 100, 1000 usw. bezeichnet.
Kartenfunktionen in einem linearen Diagramm. Sowohl die x- als auch die y-Skala messen die gleichen Einheiten. In der Abbildung ist y = f (x) in Grün daher eine gerade Linie mit einer Steigung von 1. Y = log10 (x) in Blau schneidet die x-Achse bei x = 1 und hat eine positive Steigung, die sich 0 nähert. Y = 10 ^ x in Rot schneidet die y-Achse bei y = 1 und hat eine positive Steigung, die gegen unendlich geht.
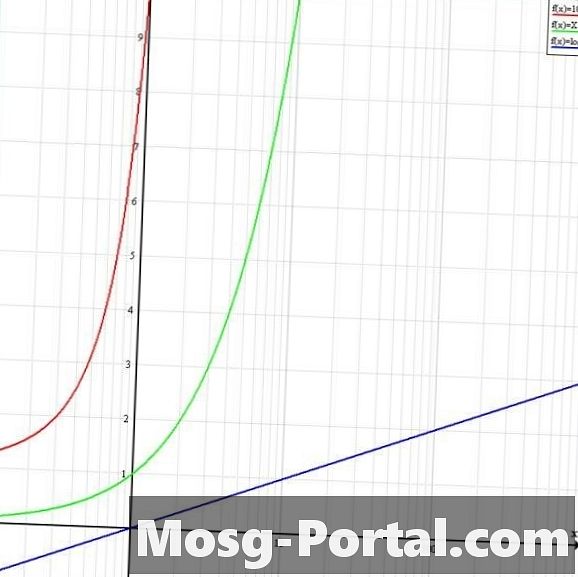
Verwenden Sie ein Lin-Log-Diagramm. Diese Art von logarithmischem Diagramm hat eine y-Achse mit linearer Skalierung und eine x-Achse mit logarithmischer Skalierung. Die Skalierung der x-Achse wird daher in Bezug auf die y-Achse um den Faktor 10 ^ x komprimiert. In der Abbildung ähnelt y = log10 (x) in Blau nun der Linie y = x im linearen Diagramm. Y = 10 ^ x in Rot schneidet die y-Achse bei x = 10 und hat eine positive Steigung, die gegen unendlich geht. Y = x in Grün sieht jetzt wie y = 10 ^ x im linearen Graphen aus.
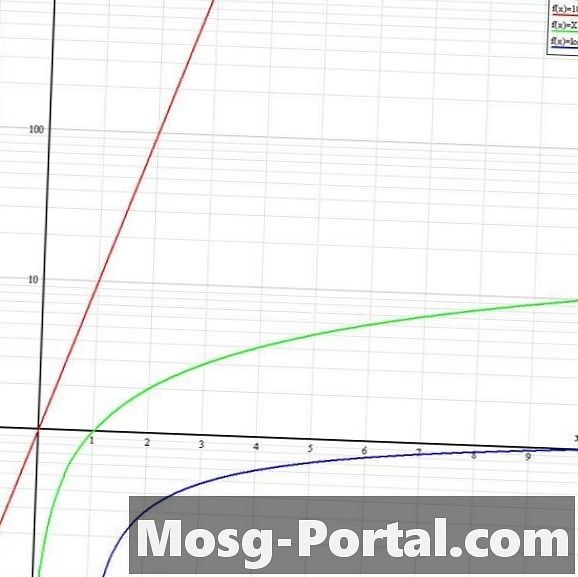
Verwenden Sie ein Log-Lin-Diagramm. Diese Art von logarithmischem Diagramm hat eine y-Achse mit logarithmischem Maßstab und eine x-Achse mit linearem Maßstab. Die Skalierung der x-Achse wird daher gegenüber der y-Achse um den Faktor 10 ^ x erweitert. In der Abbildung sieht y = 10 ^ x in Rot wie y = x in der linearen Grafik aus. Y = x in Grün sieht aus wie y = log10 (x) im linearen Diagramm, und y = log10 (x) befindet sich unter der x-Achse mit einer positiven Steigung und nähert sich der x-Achse asymptotisch.