
Autokorrelation ist eine statistische Methode zur Analyse von Zeitreihen. Der Zweck besteht darin, die Korrelation zweier Werte in demselben Datensatz zu unterschiedlichen Zeitschritten zu messen. Obwohl die Zeitdaten nicht zur Berechnung der Autokorrelation verwendet werden, sollten Ihre Zeitinkremente gleich sein, um aussagekräftige Ergebnisse zu erhalten. Der Autokorrelationskoeffizient dient zwei Zwecken. Es kann Nicht-Zufälligkeit in einem Datensatz erkennen. Wenn die Werte im Datensatz nicht zufällig sind, kann die Autokorrelation dem Analysten bei der Auswahl eines geeigneten Zeitreihenmodells helfen.
Berechnen Sie den Mittelwert oder Durchschnitt für die Daten, die Sie analysieren. Der Mittelwert ist die Summe aller Datenwerte geteilt durch die Anzahl der Datenwerte (n).
Legen Sie eine Zeitverzögerung (k) für Ihre Berechnung fest. Der Verzögerungswert ist eine Ganzzahl, die angibt, wie viele Zeitschritte einen Wert von einem anderen trennen. Beispielsweise beträgt die Verzögerung zwischen (y1, t1) und (y6, t6) fünf, da zwischen den beiden Werten 6-1 = 5 Zeitschritte liegen. Beim Testen auf Zufälligkeit berechnen Sie normalerweise nur einen Autokorrelationskoeffizienten mit der Verzögerung k = 1, obwohl auch andere Verzögerungswerte funktionieren. Wenn Sie ein geeignetes Zeitreihenmodell bestimmen, müssen Sie eine Reihe von Autokorrelationswerten mit jeweils unterschiedlichen Verzögerungswerten berechnen.
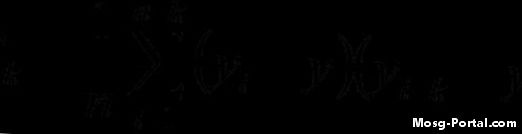
Berechnen Sie die Autokovarianzfunktion mit der angegebenen Formel. Wenn Sie zum Beispiel die dritte Iteration (i = 3) mit einer Verzögerung von k = 7 berechnet haben, würde die Berechnung für diese Iteration folgendermaßen aussehen: (y3 - y-bar) (y10 - y-bar) Durch alle iterieren Werte von "i" und nehmen Sie dann die Summe und dividieren Sie es durch die Anzahl der Werte im Datensatz.
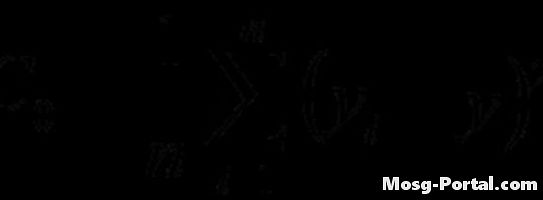
Berechnen Sie die Varianzfunktion mit der angegebenen Formel. Die Berechnung ähnelt der der Autokovarianzfunktion, es wird jedoch keine Verzögerung verwendet.

Teilen Sie die Autokovarianzfunktion durch die Varianzfunktion, um den Autokorrelationskoeffizienten zu erhalten. Sie können diesen Schritt umgehen, indem Sie die Formeln für die beiden Funktionen wie gezeigt teilen. Oft benötigen Sie jedoch die Autokovarianz und die Varianz für andere Zwecke, sodass es praktisch ist, sie auch einzeln zu berechnen.